Zero-grafico

Costruire un semplice grafico per rappresentare le frequenze di un insieme di dati è in genere una richiesta che i ragazzi di prima media riescono a gestire senza troppe difficoltà. Le “indagini” che si possono fare in classe all’inizio dell’anno, anche per conoscersi un po’, coinvolgono numeri che non presentano complicazioni per la rappresentazione (e per questo è interessante proporre qualche esercizio che chiede ad esempio di rappresentare frequenze vicine tra loro ma lontane da zero…). Eppure, anche situazioni così elementari possono far emergere fraintendimenti, come mostra questo esempio realizzato da un gruppo di alunni.

Questa è la tabella delle frequenze che risposte alla domanda: “Qual è il tuo numero di scarpe?” rivolta a un gruppo di circa 70 bambini di quinta primaria.

Ed ecco il grafico.

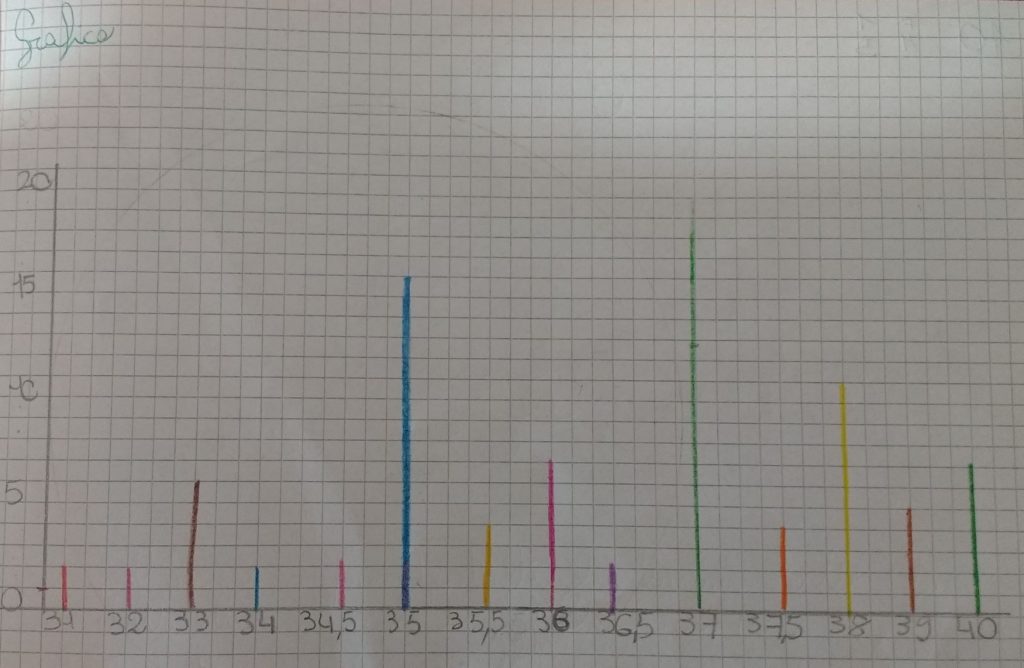
Come si può vedere (spero!) tutte linee sono più lunghe di un quadretto rispetto al dovuto; me ne sono accorto controllando i primi cinque valori, quattro dei quali sono 1. Ho aggiunto un segno rosso sull’asse verticale per indicare lo zero effettivo. Non sono riuscito a capire il motivo di questa scelta, alla domanda: “Perché avete costruito il grafico così?” ho avuto una risposta che francamente non era intellegibile in cui si vagheggiava una non meglio definita difficoltà legata allo zero.

Una rappresentazione, che pur può all’insegnante sembrare semplice, nasconde insidie.